Fermat’s last theorem: a proof for right-angled triangles
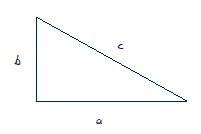
Introduction Fermat's last theorem states that no three positive integers a, b, and c can satisfy the equation: a n + b n = c n where a, b and c are real, whole integers and n > 2. The purpose of this paper is to prove Fermat’s last theorem in relation to right-angled triangles. The proof shall be by way of contradiction using algebra and geometry. I shall leave to another day whether it is possible to prove the theorem in relation to any other triangles, or indeed any other non-triangle values. Pythagoras’ theorem: the starting point We know from Pythagoras’ theorem that: c 2 = a 2 + b 2 Pythagoras’ theorem can be illustrated geometrically in the adjacent manner. A square is made on each length of the triangle. The square on the hypotenuse (c) is equal in area to the sum of the area of the squares on the other sides (a and b). But what if we decided to build a cube out of each of those squares? Would the volume of cube c be equal to the sum of the vol