Fermat’s last theorem: a proof for right-angled triangles
Introduction
Fermat's last theorem states that no three positive integers a, b, and c can satisfy the equation:
an + bn = cn
where a, b and c are real, whole integers and n > 2.
The purpose of this paper is to prove Fermat’s last theorem in relation to right-angled triangles. The proof shall be by way of contradiction using algebra and geometry. I shall leave to another day whether it is possible to prove the theorem in relation to any other triangles, or indeed any other non-triangle values.
Pythagoras’ theorem: the starting point
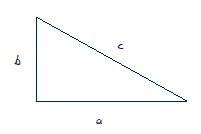 We know from Pythagoras’ theorem that:
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Pythagoras’ theorem can be illustrated geometrically in the adjacent manner.
A square is made on each length of the triangle. The square on the hypotenuse (c) is equal in area to the sum of the area of the squares on the other sides (a and b).
But what if we decided to build a cube out of each of those squares?
Would the volume of cube c be equal to the sum of the volumes of cube a and
cube b?
n=3
Let us assume that:
c3 = a3 + b3
Where c, a and b are real numbers and whole integers.

This can be illustrated geometrically in the adjacent manner.
It is important to realise that this is just a 2 dimensional representation of a 3 dimensional object: the angle at the base of each cube is 90º, however when this is represented on a flat page the angle is not capable of being drawn as 90º.
 Instead your brain interprets the drawn angles as 90º angles, aided by such techniques as shading.
Instead your brain interprets the drawn angles as 90º angles, aided by such techniques as shading.
So, back to the proof:
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Accordingly c = √(a2 + b2)
Now we can multiply both sides of Pythagoras’ equation by the value c to produce:
c3 = √(a2 + b2) (a2 + b2)
Bearing in mind our assumption c3 = a3 + b3 it follows that:
√(a2 + b2) (a2 + b2) = a3 + b3
If we square both sides we get:
(a2 + b2)3 = (a3 + b3)2
And if we factor the right side of the equation we get:
(a2 + b2)3 = (a + b) (a2 + b2 - ab) (a + b) (a2 + b2 - ab)
(a2 + b2)3 = (a2 + b2 + 2ab) (a2 + b2 - ab) (a2 + b2 - ab)
However a2 + b2 = c2 (Pythagoras theorem), thus:
(c2)3 = (c2 + 2ab) (c2 - ab) (c2 - ab)
c6 = (c2 + 2ab) (c4 - 2c2ab + a2b2)
c6 = c6 - 2c4ab + c2a2b2 + 2c4ab - 4c2a2b2 + 2a3b3
c6 = c6 - 3c2a2b2 + 2a3b3
3c2a2b2 = 2a3b3
c2 = 2/3ab
But
if c2 = 2/3ab
and c2 = a2 + b2
a2 + b2 = 2/3ab
This cannot be true. Rather, a2 + b2 > 2/3ab
Consider the 3, 4, 5 Pythagorean triple:
a2 + b2 = 9 + 16 = 25
However:
2/3ab = 8
Accordingly for a right-angled triangle where n = 3, the left side of the equation is greater than the right:
c6 > c6 - 3c2a2b2 + 2a3b3
And Fermat’s last theorem is proven in that special case.
n=4
Let us assume that:
c4 = a4 + b4
Where c, a and b are real numbers and whole integers.
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Accordingly:
c4 = (a2 + b2)2
Bearing in mind our assumption c4 = a4 + b4 it follows that:
(a2 + b2)4 = (a4 + b4)3
(a2 + b2)2 = a4 + b4
(a2 + b2) (a2 + b2) = a4 + b4
a4 + b4 + 2ab = a4 + b4
This is manifestly untrue.
For a right-angled triangle where n = 4, the left side of the equation is greater than the right, and accordingly Fermat’s last theorem is proven in that special case.
n=5
Let us assume that:
c5 = a5 + b5
Where c, a and b are real numbers and whole integers.
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Accordingly c = √(a2 + b2)
And accordingly:
c5 = √(a2 + b2) (a2 + b2)2
Bearing in mind our assumption c5 = a5 + b5 it follows that:
√(a2 + b2) (a2 + b2)2 = a3 + b3
If we square both sides we get:
(a2 + b2)3 = (a3 + b3)2
(a2 + b2)5 = (a5 + b5)2
(a2 + b2) (a4 + b4 + 2ab) (a4 + b4 + 2ab) = (a10 + b10 + 2a5b5)
(a2 + b2) (a8 + a4b4 + 2a5b + a4b4 + b8 + 2ab5 + 2a5b + 2ab5 + 4a2b2) = (a10 + b10 + 2a5b5)
(a2 + b2) (a8 + b8 + 2a4b4 + 4a5b + 4ab5 + 4a2b2) = (a10 + b10 + 2a5b5)
(a10 + a2b8 + 2a6b4 + 4a7b + 4a3b5 + 4a4b2 + a8b2 + b10 + 2a4b6 + 4a5b3 + 4ab7 + 4a2b4) = (a10 + b10 + 2a5b5)
a10 + b10 + a2b8 + a8b2 + 2a6b4 + 2a4b6 + 4a3b5 + 4a5b3 + 4a7b + 4ab7 + 4a4b2 + 4a2b4 = a10 + b10 + 2a5b5
This manifestly untrue.
For a right-angled triangle where n = 5, the left side of the equation is far greater than the right, and accordingly Fermat’s last theorem is proven in that special case.
Conclusion
From the above it is clear that as the value of n increases, the left side of the equation produces values exponentially greater than the right.
Consider how in the case of n = 3, the value for c2 = 2/3ab, in which case the left side of the equation was slightly larger than the right.
For n = 4, c2 was greater than the right by 2ab.
By n = 5, the left was greater than the right by a2b8 + a8b2 + 2a6b4 + 2a4b6 + 4a3b5 + 4a5b3 + 4a7b + 4ab7 + 4a4b2 + 4a2b4!
If you do the equations for n = 6, you'll find the left side of the equation larger yet again (relative to the right, that is) - and so it goes.
It follows that for any right-angled triangle where n > 5, the left side of the equation is going to be even greater than the right as compared to n = 5.
Accordingly Fermat’s last theorem is proven for a right-angled triangle for any value of n.
Copyright © 2010 Dejan Djurdjevic
Fermat's last theorem states that no three positive integers a, b, and c can satisfy the equation:
an + bn = cn
where a, b and c are real, whole integers and n > 2.
The purpose of this paper is to prove Fermat’s last theorem in relation to right-angled triangles. The proof shall be by way of contradiction using algebra and geometry. I shall leave to another day whether it is possible to prove the theorem in relation to any other triangles, or indeed any other non-triangle values.
Pythagoras’ theorem: the starting point
 We know from Pythagoras’ theorem that:
We know from Pythagoras’ theorem that:c2 = a2 + b2
Pythagoras’ theorem can be illustrated geometrically in the adjacent manner.
A square is made on each length of the triangle. The square on the hypotenuse (c) is equal in area to the sum of the area of the squares on the other sides (a and b).
But what if we decided to build a cube out of each of those squares?
Would the volume of cube c be equal to the sum of the volumes of cube a and
cube b?
n=3
Let us assume that:
c3 = a3 + b3
Where c, a and b are real numbers and whole integers.

This can be illustrated geometrically in the adjacent manner.
It is important to realise that this is just a 2 dimensional representation of a 3 dimensional object: the angle at the base of each cube is 90º, however when this is represented on a flat page the angle is not capable of being drawn as 90º.
 Instead your brain interprets the drawn angles as 90º angles, aided by such techniques as shading.
Instead your brain interprets the drawn angles as 90º angles, aided by such techniques as shading.So, back to the proof:
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Accordingly c = √(a2 + b2)
Now we can multiply both sides of Pythagoras’ equation by the value c to produce:
c3 = √(a2 + b2) (a2 + b2)
Bearing in mind our assumption c3 = a3 + b3 it follows that:
√(a2 + b2) (a2 + b2) = a3 + b3
If we square both sides we get:
(a2 + b2)3 = (a3 + b3)2
And if we factor the right side of the equation we get:
(a2 + b2)3 = (a + b) (a2 + b2 - ab) (a + b) (a2 + b2 - ab)
(a2 + b2)3 = (a2 + b2 + 2ab) (a2 + b2 - ab) (a2 + b2 - ab)
However a2 + b2 = c2 (Pythagoras theorem), thus:
(c2)3 = (c2 + 2ab) (c2 - ab) (c2 - ab)
c6 = (c2 + 2ab) (c4 - 2c2ab + a2b2)
c6 = c6 - 2c4ab + c2a2b2 + 2c4ab - 4c2a2b2 + 2a3b3
c6 = c6 - 3c2a2b2 + 2a3b3
3c2a2b2 = 2a3b3
c2 = 2/3ab
But
if c2 = 2/3ab
and c2 = a2 + b2
a2 + b2 = 2/3ab
This cannot be true. Rather, a2 + b2 > 2/3ab
Consider the 3, 4, 5 Pythagorean triple:
a2 + b2 = 9 + 16 = 25
However:
2/3ab = 8
Accordingly for a right-angled triangle where n = 3, the left side of the equation is greater than the right:
c6 > c6 - 3c2a2b2 + 2a3b3
And Fermat’s last theorem is proven in that special case.
n=4
Let us assume that:
c4 = a4 + b4
Where c, a and b are real numbers and whole integers.
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Accordingly:
c4 = (a2 + b2)2
Bearing in mind our assumption c4 = a4 + b4 it follows that:
(a2 + b2)4 = (a4 + b4)3
(a2 + b2)2 = a4 + b4
(a2 + b2) (a2 + b2) = a4 + b4
a4 + b4 + 2ab = a4 + b4
This is manifestly untrue.
For a right-angled triangle where n = 4, the left side of the equation is greater than the right, and accordingly Fermat’s last theorem is proven in that special case.
n=5
Let us assume that:
c5 = a5 + b5
Where c, a and b are real numbers and whole integers.
We know from Pythagoras’ theorem that:
c2 = a2 + b2
Accordingly c = √(a2 + b2)
And accordingly:
c5 = √(a2 + b2) (a2 + b2)2
Bearing in mind our assumption c5 = a5 + b5 it follows that:
√(a2 + b2) (a2 + b2)2 = a3 + b3
If we square both sides we get:
(a2 + b2)3 = (a3 + b3)2
(a2 + b2)5 = (a5 + b5)2
(a2 + b2) (a4 + b4 + 2ab) (a4 + b4 + 2ab) = (a10 + b10 + 2a5b5)
(a2 + b2) (a8 + a4b4 + 2a5b + a4b4 + b8 + 2ab5 + 2a5b + 2ab5 + 4a2b2) = (a10 + b10 + 2a5b5)
(a2 + b2) (a8 + b8 + 2a4b4 + 4a5b + 4ab5 + 4a2b2) = (a10 + b10 + 2a5b5)
(a10 + a2b8 + 2a6b4 + 4a7b + 4a3b5 + 4a4b2 + a8b2 + b10 + 2a4b6 + 4a5b3 + 4ab7 + 4a2b4) = (a10 + b10 + 2a5b5)
a10 + b10 + a2b8 + a8b2 + 2a6b4 + 2a4b6 + 4a3b5 + 4a5b3 + 4a7b + 4ab7 + 4a4b2 + 4a2b4 = a10 + b10 + 2a5b5
This manifestly untrue.
For a right-angled triangle where n = 5, the left side of the equation is far greater than the right, and accordingly Fermat’s last theorem is proven in that special case.
Conclusion
From the above it is clear that as the value of n increases, the left side of the equation produces values exponentially greater than the right.
Consider how in the case of n = 3, the value for c2 = 2/3ab, in which case the left side of the equation was slightly larger than the right.
For n = 4, c2 was greater than the right by 2ab.
By n = 5, the left was greater than the right by a2b8 + a8b2 + 2a6b4 + 2a4b6 + 4a3b5 + 4a5b3 + 4a7b + 4ab7 + 4a4b2 + 4a2b4!
If you do the equations for n = 6, you'll find the left side of the equation larger yet again (relative to the right, that is) - and so it goes.
It follows that for any right-angled triangle where n > 5, the left side of the equation is going to be even greater than the right as compared to n = 5.
Accordingly Fermat’s last theorem is proven for a right-angled triangle for any value of n.
Copyright © 2010 Dejan Djurdjevic
Comments
Yes, it's a curious problem, although not one upon which anything in particular hinges! I can see why mathematicians are so scathing of attempts to solve Fermat's last theorem.
My own attempt last year was to build on the Pythagorean triplet argument I used here. This might seem counter-intuitive, however I chose to attempt this method because it seemed to me that you're better off with as many "givens" as you can muster.
In the end, I tried to establish a proof that relies upon factorization, or rather its impossibility, if one assumes that a^n + b^n = c^n (where otherwise that factorization should be possible if the assumption were correct). I suspect it doesn't get there, but I stopped caring after a fairly short time!
You can have a look at it here.
As you can see, one "math snob" has already left a withering comment. It's interesting how condescending "experts" in any field can be when an amateur strays, however sincerely and respectfully, into their field of expertise. I've seen it in music, literature, law... you name it.
In this case this is no doubt a reaction to the many deluded people who imagine that they have some special skill that lets them circumvent proper mathematical study; and that there is some earth-shattering consequence to follow if they were, upon some miracle, to stumble upon an elementary proof of Fermat's last theorem.
That I am not one of these, but rather just "diarising" my various, stray thoughts (which in this case involved a rather impulsive look at Fermat's theorem over a couple of weeks), should be apparent from the broad range of material in my blog.
All the best!
In other words, powers of 1 and 2 for n show divisibilty and therefore imply that one and two dimensional representation are in fact not real. Whereas, powers of zero and n >2 are part of reality. The zero dimension of the point, the 3 dimension of the physical world, and the infinite dimensions of the infinite are all part of the metaphysically real. Linear and 2 dimensional representations are divisible and not real. These dimensions are unreliable in explaining our universe, so toss out the vector, plane geometry etc. We must rely only on real things like points, spheres and spherical and hyperbolic geometries.
I know I said: "where a, b and c are real, whole integers and n > 2."
But I actually should have said "whole numbers". I can't really imagine a triangle with one side that is a negative. Can you?